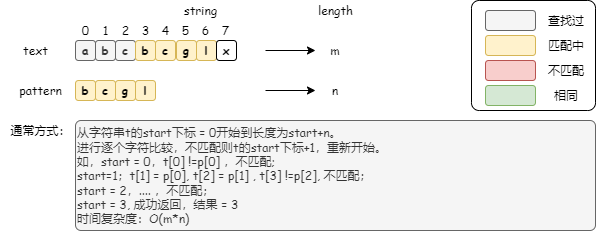
通常的字符串查找
逐个比较字符串,匹配失败重头再来。
KMP
解决字符串查找
目的:匹配失败时,模式串回退,主串不用回退
在一个字符串(S)中查找一个子串(W)出现的位置。
示例
1
2
|
text: abcxabcdabxabcdabcdabcy
pattern: abcdabcy
|
KMP思路
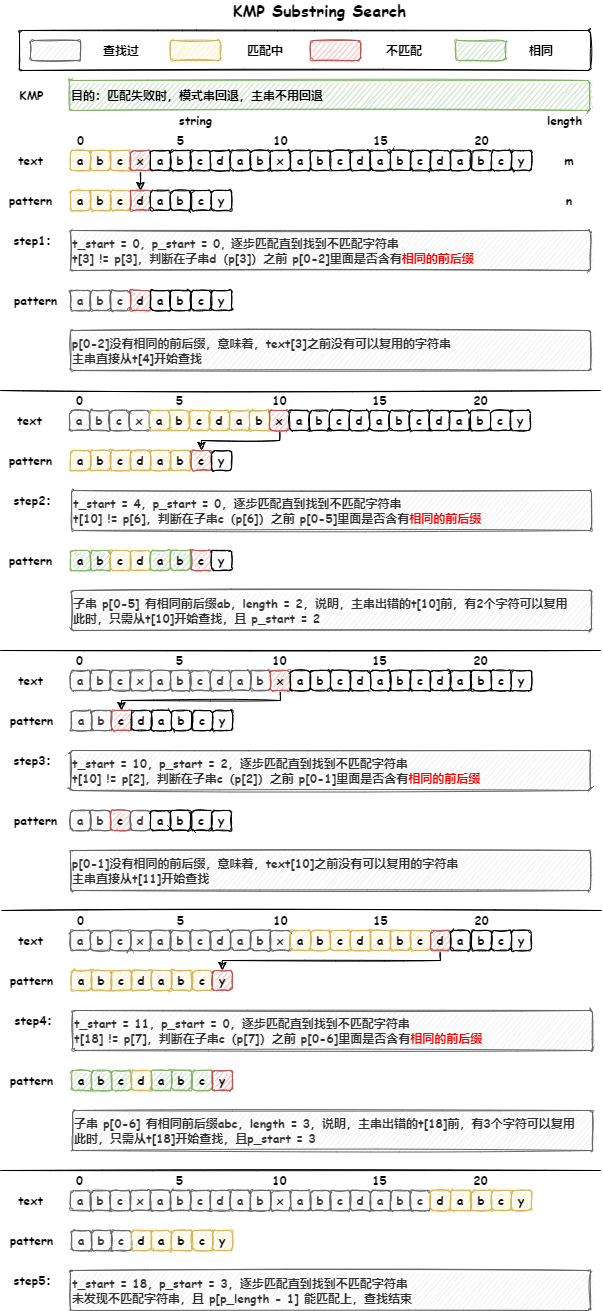
这里的p_start通常情况下,被描述为next数组,它的含义是:字符串在当前位置存在前缀后缀匹配数组的长度,也可以描述为匹配度。 当出现不匹配时,只需要知道前面的字符串的匹配度,就可以知道,下一次匹配时,pattern的开始查找位置。
信息
如 step4时,
- p_index = 7时,pattern[7] = j 与text[18] 不匹配
- 此时前面的匹配度 =next[p_index - 1] = 3
- 匹配度=3,说明对于主串text,前面 t_index = 18前面的3个字符和pattern前面的3个字符一定是匹配的
- 所以,继续查找时,d_index 还是18 不需要回退,只需要从p_index = 3开始匹配即可,如step5 所示
如何获取next数组
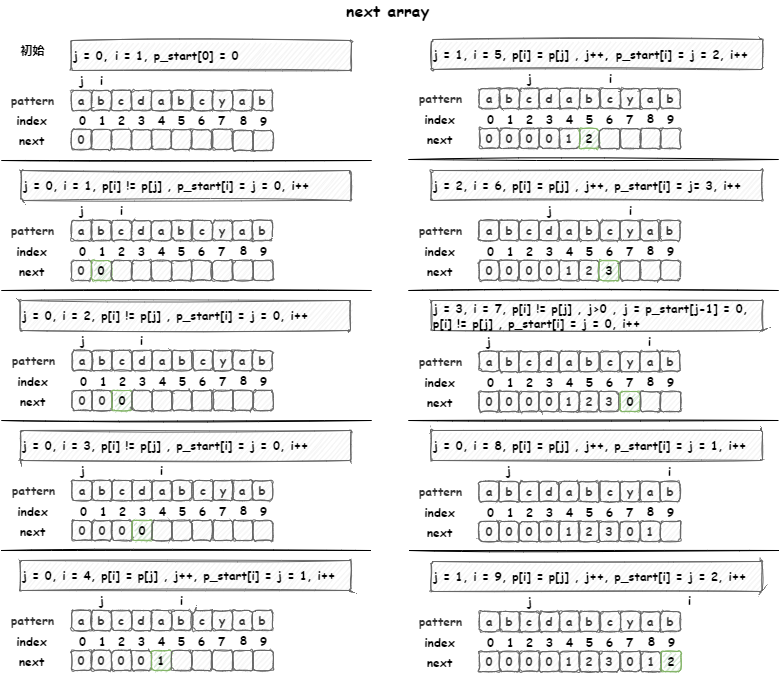
pattern为abcdabcyab时匹配度表
| index |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| pattern |
a |
b |
c |
d |
a |
b |
c |
y |
a |
b |
| next |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
int[] getNext(String pattern) {
int[] next= new int[pattern.length()];
int j= 0;
for (int i = 1; i < pattern.length(); i++) {
while (j> 0 && pattern.charAt(j) != pattern.charAt(i)) {
j= next[j- 1]; // 在子对称里面查找是否有能复用的对称
}
if (pattern.charAt(j) == pattern.charAt(i)) {
j++;
}
next[i] = j;
}
return next;
}
|
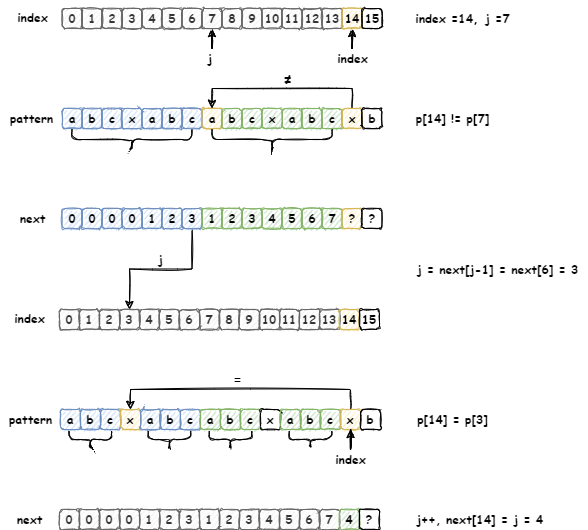
pattern为abcxabcabcxabcxb时匹配度表
| index |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| pattern |
a |
b |
c |
x |
a |
b |
c |
a |
b |
c |
x |
a |
b |
c |
x |
b |
| next |
0 |
0 |
0 |
0 |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4 |
0 |
index = 14时,前面的对称度是7 。j = 7,p[14] = ‘x’ ,此时,
- 如果要存在对称性,那么对称程度肯定比前面这个c 的对称程度小,如果大那么x就继承前面的对称性了。
- 要找更小的对称,必然在对称内部还存在子对称,而且这个x必须紧接着在子对称之后。
KMP 完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Soultion{
// 在文本 text 中寻找模式串 pattern,返回所有匹配的位置开头
List<Integer> search(String text, String pattern) {
List<Integer> positions = new ArrayList<>();
int[] next= getNext(pattern);
int count = 0;
for (int i = 0; i < text.length(); i++) {
while (count > 0 && pattern.charAt(count) != text.charAt(i)) {
// count 回退
count = next[count - 1];
}
if (pattern.charAt(count) == text.charAt(i)) {
count++;
}
if (count == pattern.length()) {
positions.add(i - pattern.length() + 1);
//找到一个就回退
count = next[count - 1];
}
}
return positions;
}
int[] getNext(String pattern) {
int[] next= new int[pattern.length()];
int j= 0;
for (int i = 1; i < pattern.length(); i++) {
while (j> 0 && pattern.charAt(j) != pattern.charAt(i)) {
j= next[j- 1];
}
if (pattern.charAt(j) == pattern.charAt(i)) {
j++;
}
next[i] = j;
}
return next;
}
}
|
解说视频




 支付宝
支付宝
 微信
微信